Gradient Descent in Machine Learning

Created in November 04, 2021

2021   ·   math   ml     ·   sample-posts  

This article covers the implementation and theoretical framework of gradient descent. Topics such as feature scaling and cross-validation are included to improve testing and training.
Most of the theoretical work presented below is based on Prof. Andrew Ng’s notes.

Theoretical Framework

The basic idea of gradient descent is to update the parameter \(\theta\) toward the steepest direction of the cost function \(J(\theta)\).
Its update rule is given by:

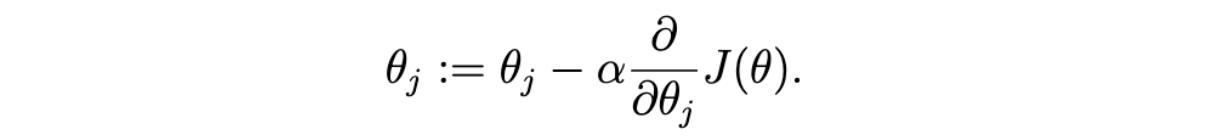
Where \(\alpha\) is the learning rate that determines the size of each update step.

The loss function \(J(\theta)\) measures how well our model fits the dataset. A common choice is the mean squared error (MSE), which is given by:

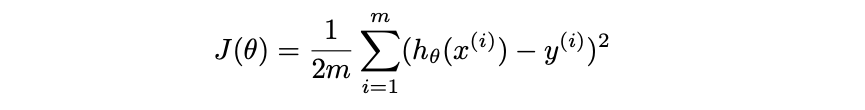
The additional 2 in the denominator simplifies the derivative later. Our task becomes minimizing \(J(\theta)\).
Taking the partial derivative of \(J(\theta)\) gives:

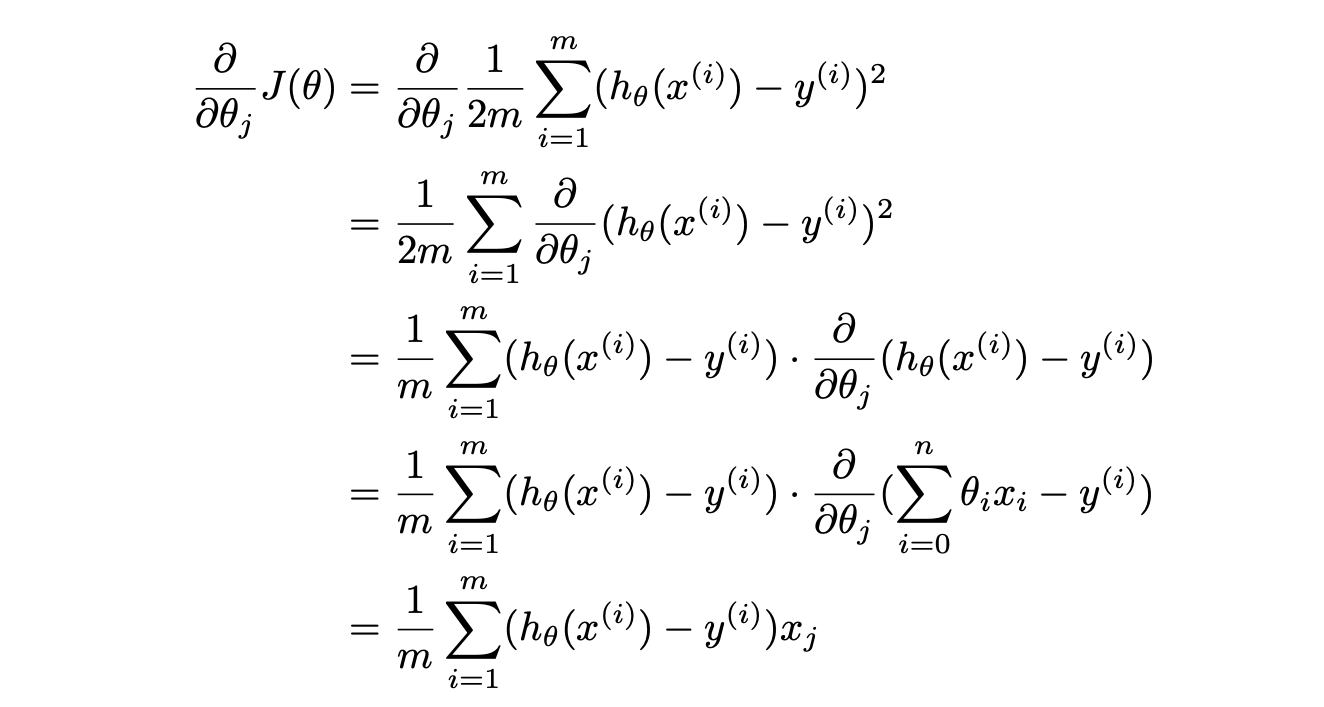
Hence, the update rule becomes:

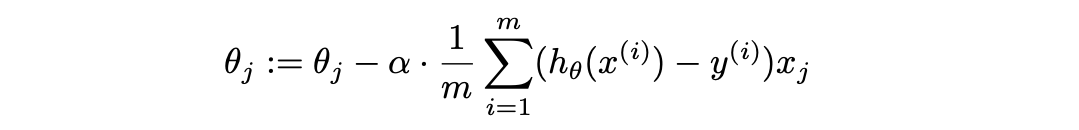
Matrix Form Update Rule

The update rule described above updates entries in \(\theta\) one at a time, making it messy to implement. Let us see how we can perform the update rule simultaneously for all entries of \(\theta\) using matrix multiplication.

Define the design matrix \(X\) as:

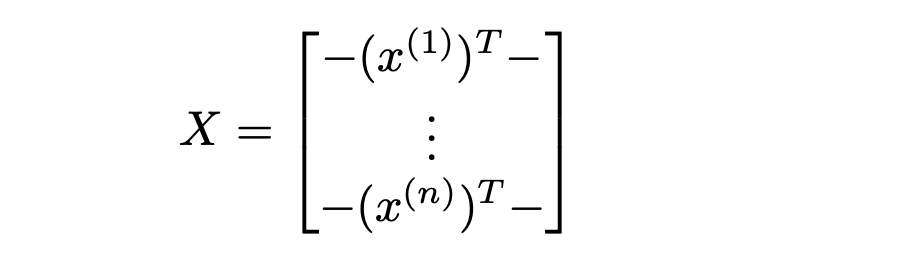
Where each row is a training example. Observe that:

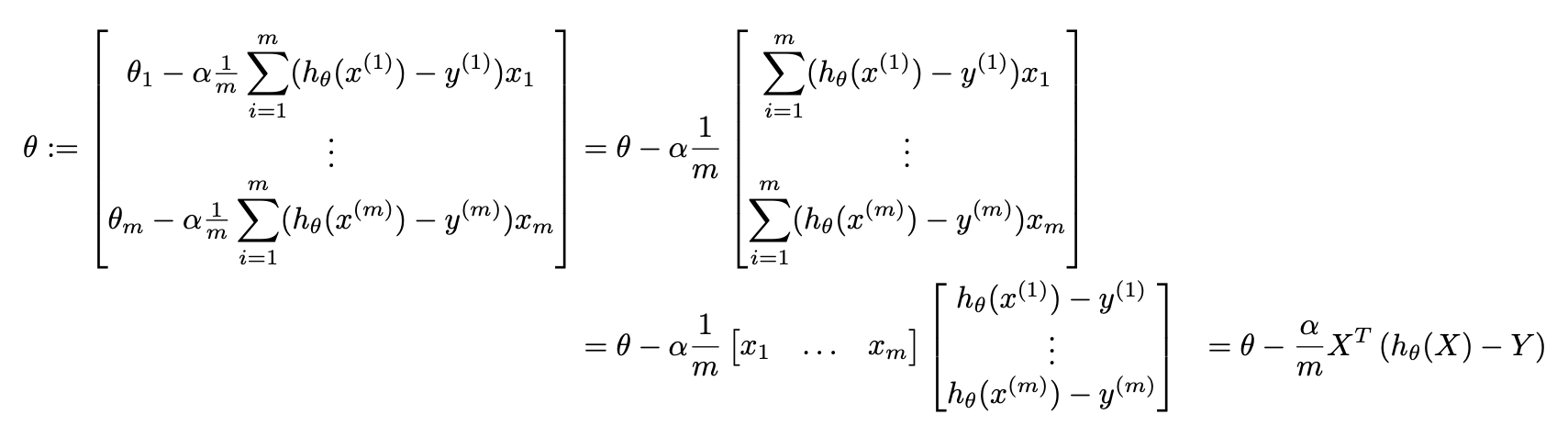
This completes the theoretical background needed to implement the gradient descent algorithm.

Implementation

Here is an implementation of gradient descent for linear regression:

Feature Scaling

To ensure proper updates, the matrix \(X\) needs to be scaled. Each element in each column of \(X\) is updated as follows:

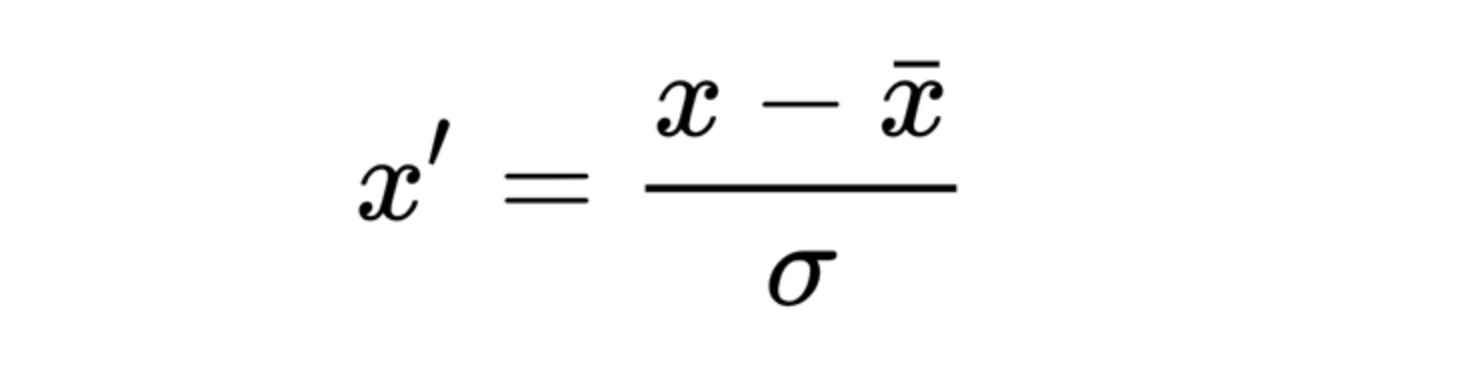
Cross-Validation

After fitting the model using gradient descent, the next step is to test its performance. A common method is cross-validation, which involves training the model on a fraction of the data and testing it on the remaining data.

K-Fold Cross-Validation
A more advanced approach is k-fold cross-validation, where the dataset is divided into \(k\) subsets. The model is trained on \(k-1\) subsets and tested on the remaining subset. This process is repeated \(k\) times, and the average testing result is calculated.

Here is an implementation: